Excel w służbie mechaniki kwantowej

Przeczytałem sobie wszystkie notki opatrzone tagiem fizyka i… nie jestem zadowolony. Miało być dostępnie dla każdego, a wyszło mimo wszystko hermetycznie. Więc dziś przestawię jedno z „klasycznych” zagadnień mechaniki kwantowej, tak, by każdy mógł sobie je wymodelować. Chodzi mianowicie o tzw. doświadczenie z dwoma szczelinami opisane choćby na blogu prof. Einego. Polega ono (mówiąc w skrócie) na tym, że cząstka przelatuje przez dwie szczeliny, by na końcu trafić w ekran. No i okazuje się, że cząstka interferuje sama ze sobą, bo na ekranie pojawią się prążki interferencyjne (widoczne jak tych cząstek puścimy dostatecznie dużo).

Na początku studiów spotkałem się z opinią, że podręczniki kursu fizyki Feynmana są wyjątkowo prosto napisane. Niemalże łopatologicznie. Zachęcony tą opinią kupiłem sobie zestaw pięciu książek i zasiadłem do lektury. Szczególnie dużo obiecywałem sobie po trzeciej (ostatniej) części kursu pod wdzięcznym tytułem „Mechanika kwantowa”. Próbowałem „wziąć ją z marszu”, ale po przebrnięciu sporej partii materiału musiałem przyznać się, że… niewiele z tego zrozumiałem. Co prawda sam Feynman twierdził: „jeśli sądzisz, że rozumiesz mechanikę kwantową, to nie rozumiesz mechaniki kwantowej”, ale marna to pociecha.

Kiedy po latach, w ramach wspominek, zasiadłem jeszcze raz do tej lektury, moją radość wywołał już pierwszy rozpatrywany przykład: doświadczenie z dwoma szczelinami. Autor wprowadził w niej wielkość 〈y|x⟩, czyli amplitudę prawdopodobieństwa[1], że cząstka przejdzie z punktu x do y. Podał nawet jak liczyć sobie te amplitudy – wzór był prosty, nic tylko usiąść do komputera i… policzyć.

Ale od początku. Otóż Feynman podaje ogólną zasadę liczenia prawdopodobieństwa: „jeśli cząstka może osiągnąć stan dwiema możliwymi drogami, całkowita amplituda jest sumą amplitud odpowiadających przejściu cząstki każdą z tych dróg z osobna”. Czyli ogólna amplituda wygląda następująco (prawdopodobieństwo to kwadrat modułu tej wielkości):

〈e|z⟩₁+〈e|z⟩₂

Przejście przez pierwszą szczelinę, to przejście z z do s1 a potem z s1 do e, z książki Feynmana dowiemy się, że trzeba pomnożyć odpowiednie amplitudy:

〈e|z⟩₁ = 〈e|s1⟩〈s1|z ⟩

Podobnie będzie dla drugiej szczeliny. Na koniec rozważań pojawia się gotowy wzór na amplitudę przejścia z punktu A do B:

〈 B|A ⟩ = exp( ip∙(r_B-r_A)/ħ) / |r_B – r_A|

No to pora liczyć. Ale do wzoru potrzebny jest pęd p. No i tu mała zagwozdka: jaki pęd? Żeby rozwikłać zagadkę, trzeba doczytać, że „źródło zawsze emituje cząstki o danej energii, więc nie będziemy potrzebować martwić się czasem”. Co między wierszami oznacza, że wzór jest zgodny ze stacjonarnym równaniem Schrödingera[2]. Dla pewności zaglądamy do innego podręcznika, gdzie podano tzw. funkcję Greena dla tego równania (dla 3 wymiarów)[3]:

G(r_A, r_B) = exp( ik|r_A-r_B|)/(4π|r_A-r_B|)

No i już wiadomo, że tam gdzie Feynman w „rozpędzie” napisał iloczyn skalarny między dwoma wektorami, wstawiamy iloczyn długości pędu[4] i odległości między punktami. Czyli wzór będzie następujący (r_AB to odległość między punktami A i B, a k=p/ħ):

〈 B|A ⟩ = exp( ikr_AB) / r_AB

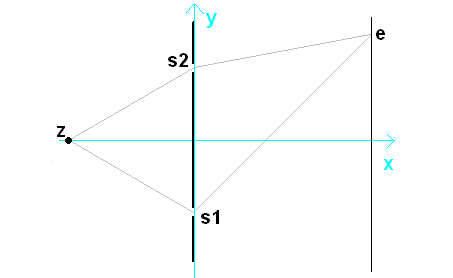
Jeśli dotarłeś do tego miejsca, to obiecuję, że już dosyć wstrętnej matematyki. Od teraz będziesz mógł poczuć się jak prawdziwy badacz mechaniki kwantowej, nawet jeśli znasz matematykę na poziomie maturalnym. Wystarczy tylko otworzyć Excela. To, co krok po kroku opiszę, to zastosowanie formuły na amplitudę prawdopodobieństwa dla przypadku przedstawionego na rysunku powyżej.

A więc zgodnie z „poprawionym” wzorem na amplitudę policzę wyrażenie na prawdopodobieństwo (kwadrat modułu amplitudy):

|〈e|s1⟩〈s1|z⟩ + 〈e|s2⟩〈s2|z⟩ |²

Excel nie ma obsługi liczb zespolonych, ale damy radę. Przede wszystkim, jeśli szczeliny leżą symetrycznie względem źródła, to wyrażenia i są takie same, więc ich udział jedynie przeskaluje rozwiązanie. Mogę więc policzyć prostszą formułę:

|〈e|s1⟩ + 〈e|s2⟩ |²

Do obliczenia będą potrzebne:

współrzędne szczelin (Y-kowe)
współrzędne punktów na ekranie: X-owa jest taka sama dla wszystkich (to odległość ekranu od szczelin)
wielkość pędu

Rozplanowałem sobie arkusz następująco: Parametry umieściłem w pierwszej kolumnie (A): pęd w komórce A2, Y-kową współrzędną pierwszej szczeliny w A4, współrzędną drugiej szczeliny zapisałem w A6 jako

=-A4

żeby było symetrycznie. Ostatni parametr, czyli odległość ekranu od szczelin wstawiłem do A8.

Ponieważ obliczenia mają być zrobione dla iluśtam punktów ekranu w kolumnie B umieściłem współrzędne Y-kowe ekranu (wartości wpisywałem od drugiej linii, żeby pierwszą mieć na opisy, co zresztą widać na dołączonym poniżej obrazku).

Teraz pora na obliczenie odległości między szczelinami a ekranem. Jest to pierwiastek z sumy kwadratów kawałka pionowego i poziomego (twierdznie Pitagorasa). W kolumnie C wstawiłem wyrażenie:

r₁=√( (x_s1-x_e)² + (y_s1-y_e)² )

co (pamiętając, że x_e=0) jest zrealizowane dla pierwszej komórki C2 jako:

=PIERWIASTEK( $A$8*$A$8 + ($A$4- B2)*($A$4- B2) )

resztę pól załatwiłem samokopiowaniem – podobnie można zrobić dla reszty kolumn. Potem przyszła pora na obliczenie fazy eksponenty:

exp( ikr₁ )

czyli w kolumnie D (nazwanej faza1), a dokładniej w komórce D2 pojawiło się:

=$A$2*C2

Pora na obliczenie exp(ikr₁)/r₁. Jak obliczyć taką eksponentę? Trzeba wiedzieć, że

exp(iα) = cos(α) +isin(α)

Już bez dokładnego analizowania napiszę, że część rzeczywista amplitudy to (oznaczyłem to sobie jako re1, kolumna E, wartość dla komórki E2):

=COS(D2)/C2

a urojona (im1 w kolumnie F, komórka F2):

=SIN(D2)/C2

Podobnie przeliczam r2, faza2, re2, i im2 (w kolumnach G, H, I, J). Końcowy wynik to zwykły kwadrat modułu sumy dwóch liczb zespolonych

|ψ|² = (re1+re2)²+(im1+im2)²

czyli w Excelu będzie to (kolumna K):

=(E2+I2)*(E2+I2) + (F2+J2)*(F2+J2)

Na koniec trzeba wstawić wykres typu XY wykorzystując kolumny B i K. Wygląda to tak:

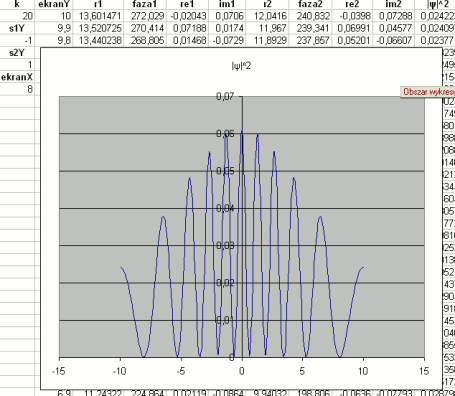
Zachęcam do samodzielnych eksperymentów parametrami. I na tym kończę ten przydługi wpis.

[1] Amplituda prawdopodobieństwa, to liczba zespolona, jaką od biedy moglibyśmy nazwać „pierwiastkiem z prawdopodobieństwa”.

[2] Czyli tak naprawdę symulujemy rozwiązanie stacjonarnego równania Schrödingera dla energii E=p²/2m. Feynman tego dokładnie nie objaśnia.

[3] Dlaczego taka funkcja i skąd ona wynika to temat na dłuższą opowieść i to na dość zaawansowanym poziomie.

[4] Dokładniej to długośc tzw. wektora falowego, czyli „przeskalowanego pędu”: k=p/ ħ. W dzisiejszych rozważaniach stała Plancka we wzorze występuje tylko tam gdzie mamy pęd. Kiedy dojdę do Excela, to będę pisał k zamiast p.