Uprzedzam, że notka epatuje wzorami, choć tak naprawdę wcale nie tymi najgorszymi. Czytelników o wrodzonej/nabytej niechęci do wyprowadzeń z góry przepraszam. Mam nadzieję, że treść wynagrodzi niewygody przy czytaniu.
O tytule
Jest (było przynajmniej wtedy, gdy bywałem jeszcze na IV piętrze) takie powiedzonko fizyków: „Z dokładnością do dziedziny”. Trudno mi jednoznacznie wskazać na źródło tego powiedzenia, ale pasuje ono w 100% do sytuacji panującej w mechanice kwantowej.
Jeden z postulatów mechaniki kwantowej mówi, że mierzonym wielkościom fizycznym odpowiadają operatory samosprzężone działające na przestrzeni stanów. Przykładowo operator pędu to różniczkowanie:
px = –iħ(∂/∂x)
No i ładnie, tylko, że operator ten „nie umie” działać na funkcje falowe nieróżniczkowalne, a takie też są w przestrzeni stanów, czyli zbiorze funkcji całkowalnych z kwadratem. Szczęśliwie dziedzina tego operatora jest na tyle duża, że wzory gdzie ten operator występuje mają sens. Czyli owe wzory są poprawne „z dokładnością do dziedziny” operatora.
W iluśtam książkach z fizyki możemy natrafić na „dowody”, uproszczenia i rozmaite formalne wyprowadzenia. Uzasadnienie jest proste: gdyby to zrobić ściśle, wynik wyjdzie taki sam, ale wyprowadzenie zajmie 10 razy więcej miejsca. Przykład? Typowy „dowód”, że operator pędu px jest samosprzężony, polega na całkowaniu przez części, czyli pokazaniu, że dla każdych dwóch funkcji falowych χ, ψ zachodzi:
(pxχ, ψ) = (χ, pxψ)
co jawnie wygląda tak:
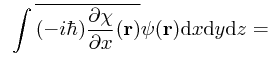
= tu trzeba to całkowanie przez części zrobić = (człony powierzchniowe równe 0) +
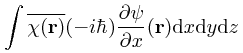
A przecież powyższa równość nie zachodzi dla każdych funkcji, tylko dla tych co są różniczkowalne. Oczywiście te bardziej zaawansowane podręczniki wprowadzają dość skomplikowaną i cokolwiek subtelną maszynerię matematyczną pozbawioną mielizn i nieścisłości.
Pora na niespodziankę
Ci którzy studiowali kwanty niech sobie przypomną jak wyglądają operatory momentu pędu. Na przykład składowa momentu pędu w kierunku osi Z jest następująca:
lz = –iħ[x(∂/∂y) – y(∂/∂x)]
jak się ją przeliczy np. we współrzędnych sferycznych (r, φ, θ), to dostaniemy:
lz = –iħ(∂/∂φ)
Można łatwo znaleźć wektory własne tego operatora[1]:
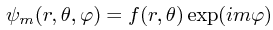
gdzie m=0, ±1, ±2, ±3… Wystarczy sprawdzić:
lz ψm = mħ ψm
W zapisie braketowym wygląda to tak:
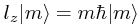
Aż się prosi, by z tym operatorem jakoś powiązać operator mnożenia przez kąt φ[2]. Obliczmy teraz komutator obu operatorów, co jest jeszcze łatwiejsze:
[φ, lz] f = –iħφ(∂/∂φ)f + iħ(∂/∂φ)(φ f) =
= –iħφ(∂f/∂φ) + iħφ(∂f/∂φ) + iħf(∂φ/∂φ) = iħf
ponieważ działanie odbywało się dla dowolnej funkcji f, można zapisać, że:
[φ, lz] = iħ
A na koniec przedstawienia policzmy wartość średnią komutatora w którymś ze stanów własnych. Użyję zapisu braketowego i wykorzystam fakt, że lz jest samosprzężone. Najpierw lewa strona równości:
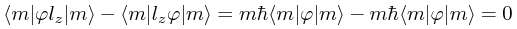
Potem prawa:
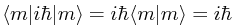
No i się nie zgadza. Gdzie błąd? Wyprowadzenia wydają się OK.
Skąd taka skucha?
Spotkałem się z wyjaśnieniem, że o ile operator lz=–iħ(∂/∂φ) jest dobrym operatorem momentu pędu (jednej składowej) o tyle samo φ z punktu widzenia fizyki jest niedobre, bo obserwabla kąta nie ma sensu w mechanice kwantowej. Wyjaśnienie jak wyjaśnienie – trochę „machanie rękami”[3]. A co mówi na ten temat matematyka?
W komutatorze [φ, lz] mamy wyraz iħ(∂/∂φ)φ. Operator taki najpierw mnoży funkcję falową przez nieciągłą funkcję kąta: po tej operacji dostaniemy zwykle nieciągłą funkcję, z którą operator różniczkowania sobie już nie poradzi. Wyjątek stanowią tylko te funkcje falowe, dla których ψ(φ=0)= ψ(φ=2π)=0. Ale ta dziedzina jest „za mała”, żeby formalne obliczenia były „prawdziwe”.
Są ciekawe konsekwencje powyższego przykładu
Po pierwsze nie ma prostej drogi na kwantowanie modeli wyrażonych we współrzędnych uogólnionych. Wspomniałem o tym przy okazji pogaduszek o układzie kartezjańskim. Skutkiem tego cały potężny aparat kawałka mechaniki klasycznej operujący na torusach (powstają one właśnie przez wprowadzenie współrzędnych typu działanie-kąt), który stanowi dziś choćby jeden ze sposobów badania chaosu deterministycznego, staje się dla mechaniki kwantowej niedostępny.
Powyższa zagwozdka pojawia się również w nietypowym modelu kwantowym, w którym istnieją stany o ściśle określonym pędzie i skończonej nieoznaczoności „położenia”. Taki jest choćby model elektronów swobodnych (matematycznie równoznaczny opisanemu w niniejszej notce), w którym ze względu na wygodę utożsamiono przeciwległe ściany. Model ten ma znaczenie przede wszystkim rachunkowe i nie wszystkimi jego konsekwencjami trzeba się przejmować – stanowi on dość zgrubne przybliżenie rzeczywistości: w końcu zapętlenie ścian pomija np. wszelkie zjawiska powierzchniowe.
No i morał na dziś: Podejście „z dokładnością do dziedziny” nie zawsze się sprawdza. Nieco naiwne podejście fizyków, że matematyka dobrze odzwierciedla intuicje wynikające z samej fizyki, zwykle wystarcza, ale czasami może zwieść na manowce.
[1] Znana sprawa, część zależna od kąta φ, to nic innego jak kawałek harmoniki sferycznej.
[2] Dowód, że jest to operator samosprzężony jest na tyle łatwy, że zostawiam jako zadanie do domu. Jako że to operator ograniczony jego dziedziną jest cała przestrzeń stanów.
[3] Skoro x i y są dobrymi obserwablami, to dlaczego arctg(y/x) nie może taką być?

