Przester to efekt, który znają bodaj wszyscy gitarzyści. Podłącza się gitarę do wzmacniacza i podkręca głośność. Jak za bardzo podgłosimy, głośnik zaczyna charczeć. Skąd się bierze to zjawisko? Wzmacniacze nie są do końca liniowe i kiedy sygnał wejściowy jest zbyt wysoki, to na wyjściu są zniekształcenia. Jeśli charakterystyka wzmacniacza jest taka jak na rysunku poniżej (sygnał wejściowy należy tak „przesunąć”, by wartość jego zerowa odpowiadała temu czerwonemu punktowi):
to sygnał wejściowy postaci:
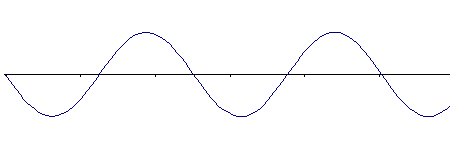
jest przetwarzany do postaci:
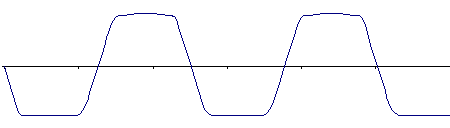
Ponieważ wzmacniacz nie może już wzmocnić podanego sygnału (tam właśnie krzywa się nasyca) maksymalne i minimalne wartości zostają „spłaszczone”. Pamiętajmy, że to wybitnie poglądowe obrazki, gdzie „zapomniano” o wielu szczegółach. Ale zasada jest mniej więcej taka[1].
Zjawisko przesterowania jest wysoce niepożądane, jeśli chodzi o sprzęt HiFi, ale w przypadku gitarzystów rockowych, jest to często wykorzystywany efekt – brzmienie gitar staje się brudniejsze, ostrzejsze, mocniejsze.
Ponieważ tytuł notki mówi o jakimś modelu, więc zamodeluję taki super ostro przesterowany dźwięk przez przebieg prostokątny. Można go sobie wyobrazić jako maksymalnie przesterowany sygnał, złożony z samych spłaszczeń. [2]. To bardzo uproszczony model, ale pozwoli on choćby na przetestowanie aparatu matematycznego.
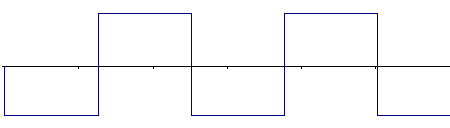
Jakie harmoniczne znajdziemy w takim sygnale? Odpowiada na to pytanie tzw. analiza harmoniczna. Okazuje się, że każdą (wystarczająco dobrą) okresową funkcję można rozłożyć na sumę sinusów:
f(t) = c0 + ∑n cnsin(nωt + φn)
gdzie ω=2π/T (T – okres funkcji) a φn to przesunięcie fazowe każdej składowej. Matematycy wolą operować jednak wzorem, gdzie efekt przesunięcia fazowego realizowany jest przez złożenie sinusów i kosinusów:
f(t) = ∑n ancos(nωt) + bnsin(nωt)
Wtedy mając an i bn można wyliczyć cn = √((an)2+(bn)2). Skąd wziąć współczynniki an i bn? Obliczając całki:
an ~ ∫[0,T] f(t)cos(nωt)dt
bn ~ ∫[0,T] f(t)sin(nωt)dt
Całkowanie odbywa się po odcinku (0, T). Wzory te wymyslili niezaleznie od siebie Euler i Fourier. Ominąłem stałe przed całkami, bo interesują nas wzajemne proporcje składowych. Akurat w przypadku przebiegu prostokątnego łatwo te całki wyliczyć (parzystych składowych nie będzie, a nieparzyste są proporcjonalne do 1/n). Skoro jednak próbuję zaprząc Excela do obliczeń, zamiast liczyć całki wyliczę sumę, czyli przybliżenie całki. Podzielę okres na ileś punktów (w moim testowym przypadku było to 400 punktów – 200 pierwszych miało wartość 1 a 200 drugich -1) i zesumuję dla kilku pierwszych n wartości f(t)sin(nt) i f(t)cos(nt) – ω jest wtedy równa 1.
f(t) czyli wartości 1 i -1 umieściłem w kolumnie C. Zmienna t wpisana jest w kolumnie B: Pierwsza wartość to 0 w komórce B2 – następne liczone są następująco:
=B2+2*PI()/$A$2
(reszta wartości dana przez samokopiowanie). Jak widać wartość zmiennej t zmienia się od 0 do 2π, czyli ω =1. W komórce A2 zliczyłem ile mamy wartości funkcji:
=SUMA(ILE.NIEPUSTYCH(C:C))
Ponieważ pierwszy wiersz zostawiłem pusty mogę tam umieścić wartość n. Np. n=1 wpisałem do D1. Teraz pora na obliczenie odpowiednich sinusów (kolumna D):
=SIN(D$1*$B2)
i iloczynu f(t)sin(nt) (kolumna E):
=D2*$C2
Podobnie liczę kosinusy (kolumna F) i f(t)cos(nt) (kolumna G). Samokopiowanie przeliczy te wyrażenia dla każdego t i można sumować. Osobno F i G[3] – będą to współczynniki b1 i a1 z których obliczymy c1.
Samokopiowanie dla wartości dla n=2, 3, 4 itd. wyprodukuje wyniki dla kolejnych składowych, które przedstawiam na wykresie cn(n):
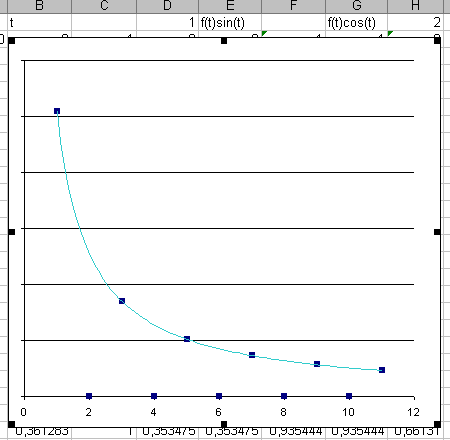
Dołożyłem linię pokazującą wykres funkcji c1/n – obliczone składowe nieparzyste „na oko” są proporcjonalne do 1/n, a parzyste równe zero.
I tak model wyprodukował nam wyniki. Co prawda nie odpowiada on na pytanie czy ostrość dźwięku zależy od istnienia dysonansowych składowych n=7,9,11... (choć te są akurat nieparzyste) czy dlatego że w ogóle dużo w nim wysokich alikwotów. Tym bardziej, że ten dźwięk nie jest jakiś strasznie ostry. Ale jak już napisałem, model jest maksymalnie uproszczony, więc trudno wyciągać z niego ostateczne wnioski. Trzeba więc będzie to sprawdzić doświadczalnie. Tradycyjnie w następnym odcinku.
[1] Gdyby to było takie proste, to dobre wzmacniacze do gitar nie kosztowałyby krocia, bo każdy mógłby sobie sam taki zrobić. A tak, słyszy się czasami, że nic nie podrobi lampowego Marshala.
[2] Jak kiedyś słyszałeś taki rodzaj dźwięku, to pewnie od razu zakrzykniesz, że nie ma on wiele wspólnego z brutalnym przesterem gitary. Przebieg prostokątny przypomina natomiast dźwięki wydawane przez starożytne gry komputerowe, albo jakieś inne dźwięki rodem z filmów s-f lat 60-tych. Mimo to dobrze jest czasami zbudować sobie taki model, żeby wyliczyć to i owo, oraz mieć jako takie pojęcie co się święci.
[3] Suma wartości G – czyli f(t)cos(nt) – powinna dać zero, ale nie daje bo metoda jest nie do końca dokładna. Można ten wynik nieco poprawić, ale formuły stałby się skomplikowańsze.

