Chyba najczęściej rozpatrywanym przypadkiem w fizyce jest oscylator harmoniczny. Nawet licealiści uczą się, jak wygląda ruch wahadła matematycznego. Kwantolodzy również często korzystają z tego modelu, rzecz jasna w wersji kwantowej. Pora więc na obrazki przedstawiające ten kwantowy ruch.
W przypadku klasycznym, kiedy przychodzi do rozwiązywania równań, przekształcamy równania Newtona (np. dla wahadła matematycznego) do postaci:

Parametr ω zależy od szczegółowych warunków zagadnienia (np. od długości wahadła i przyspieszenia ziemskiego), ale dla rozwiązania równań taka wersja wystarcza, szczególnie, że ω ma sens częstości kątowej takiego ruchu. W kwantologii jest podobnie. Przy pisaniu równania Schrödingera wstawiamy energię potencjalną postaci: V(x) = (1/2) mω2x2, niezależnie od tego jaka jest natura oddziaływań powodujących drgania.
Teraz równanie Schrödingera wygląda następująco:

Przy założeniu, że poruszająca się paczka falowa jest stanem gaussowskim, takim jak w poprzednich dwóch omawianych przypadkach, dostaniemy równania różniczkowe na M i b:
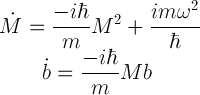
Po przeprowadzeniu obliczeń, dostałem na pierwszy rzut oka dość skomplikowane rozwiązanie:
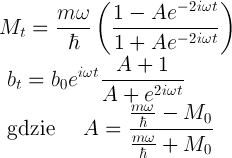
W tym skomplikowaniu widać, że oba parametry będą sobie oscylować z częstością 2ω, bo zależność od czasu przejawia się w wyrażeniach exp{-2iωt}. Zamiast jednak analizować „na sucho” co z tych wzorów wynika, zrobię to, jak już uzyskam ruchome obrazki.
Zauważmy jednak, że jeśli dobierzemy szerokość paczki falowej tak, by: M0=mω/ħ, oba rozwiązania znacząco się uproszczą:
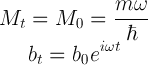
Jak podstawię sobie te parametry do wzoru na paczkę gaussowską, to się okaże, że można ją zapisać nieco inaczej, używając klasycznych parametrów położenia q i pędu p:

gdzie q i p zmieniają się tak, jak w klasycznym oscylatorze harmonicznym. Dla b0=ip0/ħ (położenie zerowe, maksymalny pęd) ruch będzie następujący:

I mamy niespodziankę! Dla stanów dobranych tak by „pasowały” do ω i m, ruch kwantowy pokrywa się z ruchem klasycznym. Parametry p i q będą zmieniać się tak samo jak w mechanice klasycznej, wszelkie inne parametry paczki falowej pozostają stałe. Żeby podkreślić, że stany gaussowskie dla których M=mω/ħ są „dopasowane” fizycy używają słowa koherentne.
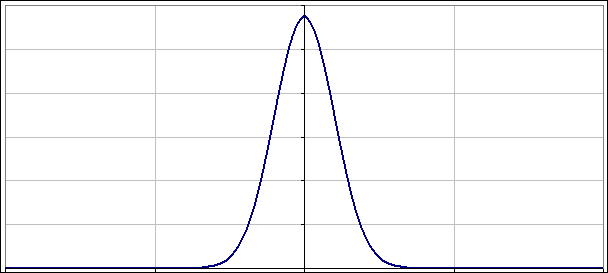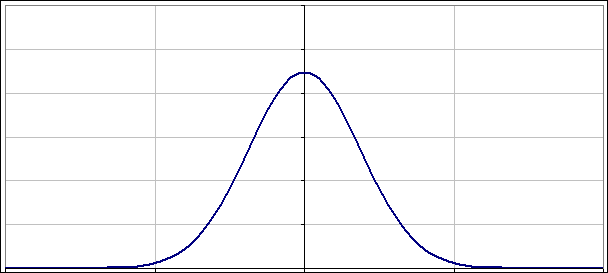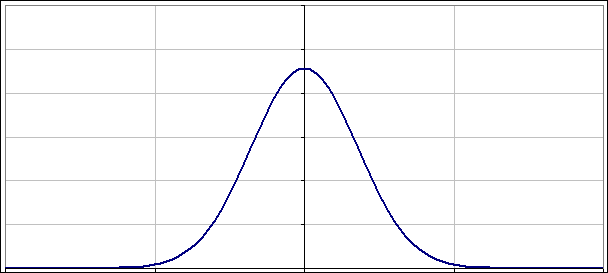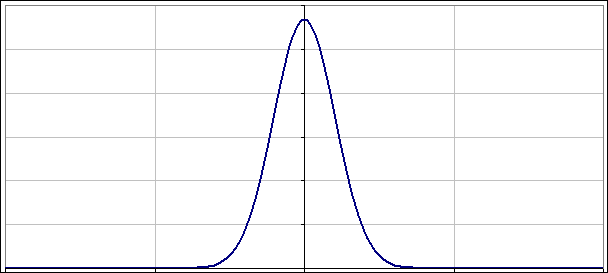
Na wykresie widać, jak paczka falowa oscyluje jak każdy przyzwoity oscylator - na osi poziomej mamy położenia:
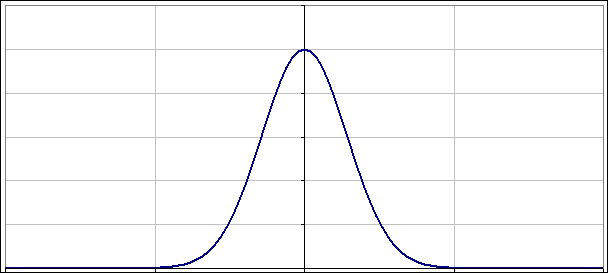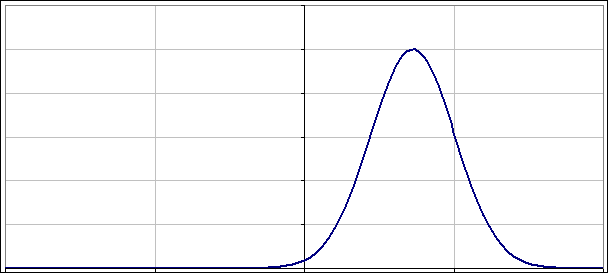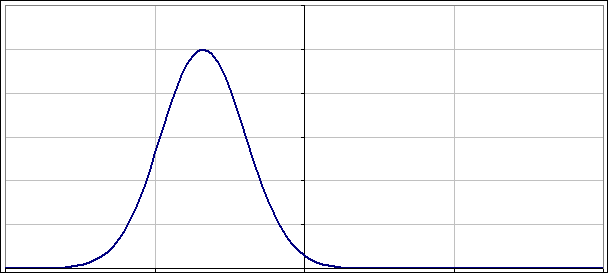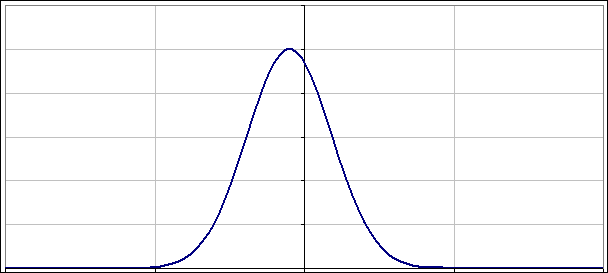
Stany koherentne są stanami gaussowskimi o rzeczywistym M. Mają więc jeszcze jedną przyjemną właściwość: minimalizują zasadę nieoznaczoności Heisenberga dla położenia i pędu. Ponieważ są parametryzowane położeniami i pędami, istnieje duża pokusa by traktować je jako odpowiedniki stanów klasycznych. Te miłe cechy stanów koherentnych powodują, że wielu fizyków bardzo je lubi.
A co z takimi co nie są „dopasowane”? Jak napisałem powyżej nie warto przegryzać się przez uzyskane rozwiązania. Lepiej po prostu popatrzeć na to jak zmienia się |ψ(x)|2 w czasie. Poniżej dwa obrazki pokazujące jak oscylują paczki falowe, gdy nieoznaczoność położenia (albo pędu) nie jest „dopasowana”:
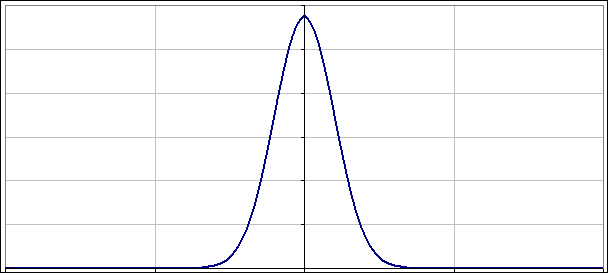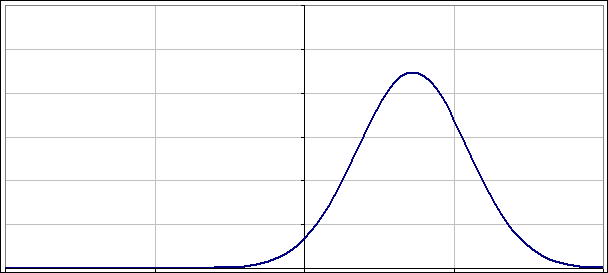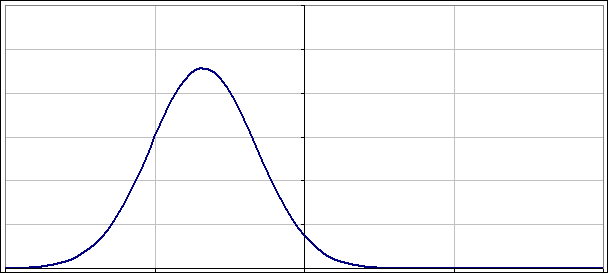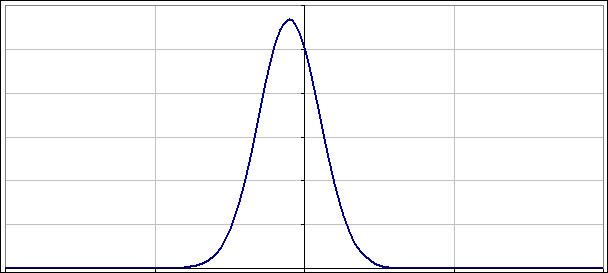
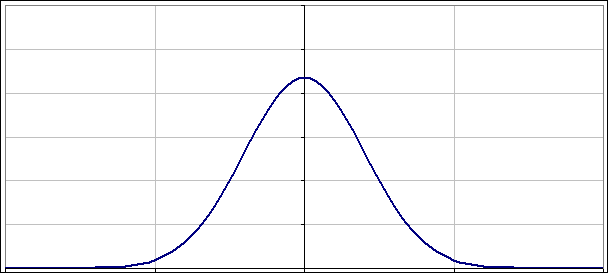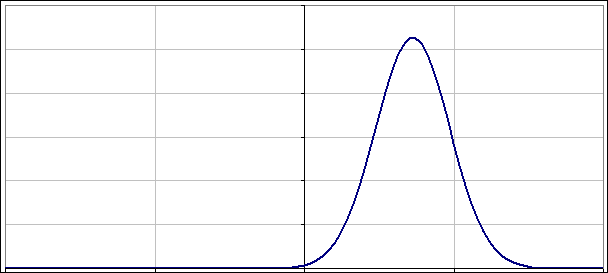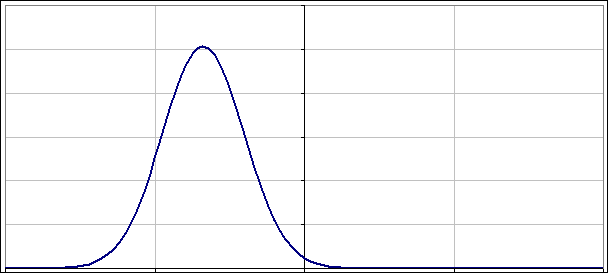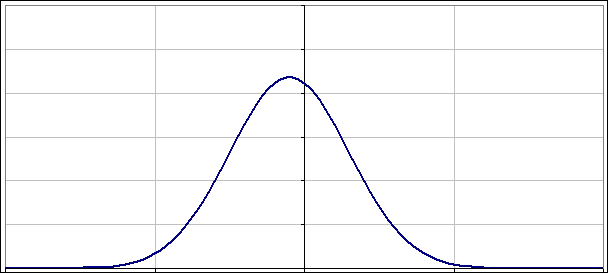
No to jeszcze na sam koniec, „niedopasowana” paczka falowa o zerowym położeniu (wykres jest „wyśrodkowany”) i zerowym pędzie, choć oba są „zerowe” na tyle, na ile pozwala im zasada nieoznaczoności: