Kwantowe odbijanie się od ścian (obrazki)

Skoro pokazałem trzy przypadki ruchu paczek falowych, pora na bonusowy, czwarty przykład. Model dotyczy cząstki odbijającej się od ścian. Paczka się odbije i… ale to zobaczymy na końcu. Na początek niestety trzeba będzie przebrnąć przez ciężkawy formalizm matematyczny. Można jednak od razu przejść na koniec notki, żeby sobie pooglądać prygotowany filmik.

Pomysł na rozwiązanie tego przypadku pokazał na jednym z wykładów prof. (wtedy dr) Marek Wolf. Na czwartym piętrze, a może i na piątym.

Rozwiązanie równania Schrödingera

Paczka falowa odbijająca się od równoległych ścian. Zagadnienie ograniczę do jednego wymiaru, zakładając, że owe ściany, w płaszczyźnie Y i Z, są wielkie i że zachowanie paczki (będzie się rozpływać jak cząstka swobodna) w tych kierunkach mnie nie interesuje. Nazywa się to jednowymiarowa nieskończona studnia potencjału. Tak dobiorę układ współrzędnych w X, by początek ściany miał współrzędną 0. Wtedy położenie drugiej ściany L, będzie jednocześnie szerokością studni.

Może ominę dyskusję jak powinien wyglądać potencjał siły V(x), zostawiając jedynie wniosek końcowy: Wpływ studni uwzględniamy przez ograniczenie na nasze funkcje falowe. Na początku i na końcu studni funkcja falowa równa jest zero. Oznacza to, że cząstki nie przenikają przez ściany, odbijając się całkowicie. Zauważmy też, że pomiędzy ścianami cząstka jest swobodna, czyli równanie Schrödingera zapiszemy w postaci:

$iħ {∂ ψ(x,t)/∂ t} = {-ħ^2/2m} {∂^2/∂ x^2}ψ(x,t) gdzie \forall t: ψ_t(0)=ψ_t(L)=0$

Jak to rozwiązać? Skorzystać z pewnego ogólnego twierdzenia. Równanie Schrödingera możemy zapisać skrótowo:

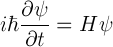
iħ{∂ψ/∂t} = H ψ

Wtedy H nazywa się operatorem energii albo Hamiltonianem. Zwykle rozwiązanie równania:

Hφn = En φn

jest łatwiejsze. Szukane w tym równaniu są E_n czyli energie i φ_n zwane wektorami własnymi energii. Równanie to nazywa się stacjonarnym równaniem Schrödingera. Jak uda nam się je rozwiązać, to możemy napisać rozwiązanie równania z czasem. Użyłem sformułowania „napisać rozwiązania” a nie „rozwiązać”, bo „napisane rozwiązanie” rzadko kiedy daje się przeliczyć do satysfakcjonującej postaci.

Najpierw znajdujemy rozkład stanu początkowego:

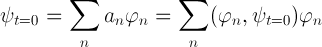
$ψ_{t=0} = \sumn an φn = \sumn (φn, ψ_{t=0}) φn$

(wyrażenie (φ_n, ψ_t₌₀) oznacza iloczyn skalarny) a potem piszemy rozwiązanie:

$ψ_t =\sumn e^{-iEn t/ħ} an φn$

Jak ktoś nie wierzy, niech podstawi to do czasowego równania Schrödingera.

Żeby wykorzystać to twierdzenie, musimy znaleźć energie i wektory własne operatora H. Dla Hamiltonianu cząstki swobodnej (a taka ona jest pomiędzy ścianami):

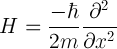
$H={-ħ/2m}{∂^2/∂ x^2}$

rozwiązaniami równania Hφ=Eφ są sinusy i kosinusy. Jak nałożymy na nie warunek warunek ψ(0)=ψ(L)=0 otrzymamy:

$φn(x)=\sin(kx), gdzie k=nπ/L, oraz En={k^2ħ^2/2m}$

Teraz można przystąpić do obliczeń. Trzeba będzie:

Wybrać jakiś stan początkowy. Według mnie najlepiej, podobny do gaussowskiego, żeby mieć jasną interpretację jaki jest pęd i położenie. Przy okazji trzeba się zastanowić jakie powinny być parametry paczki falowej, żeby zabawa miała sens.
Obliczyć sobie współrzędne: a_n=(φ_n, ψ_t₌₀).
Obliczyć sobie jak zmienia się faza każdej współrzędnej: exp{-iE_nt/ħ}.
Przemnożyć jedno przez drugie, żeby znaleźć fazy przy każdej składowej po czasie t.
Narysować wykres, dodając składowe (sinusy) pomnożone przez obliczone fazy dla tylu x, żeby wykres był czytelny. We wzorze suma jest nieskończona więc jej nie wykonamy, ale jak zesumujemy kilkadziesiąt składowych, dostaniemy co potrzeba, pod warunkiem, że odpowiednio dobierzemy stan początkowy.
Odnaleźć Małego (żeby powiedzieć mu, że znalazłem Królika). „Z czego wynika, że zanosi się na bardzo kłopotliwy dzień”…

To ostatnie to żart.

Zaraz skończę z bezwstydnym opisywaniem stosowanej matematyki, tylko jeszcze parę słów o tym stanie początkowym. Najlepiej wziąć sobie stan podobny do gaussowskiego: ψ(x, t=0) =exp{M(x-q)²/2+ipx/ħ}. Wielkości M i q trzeba dobrać tak by otrzymać paczkę falową prawie równą zero na końcach studni (jest to możliwe bo exp{-x²} jest bardzo szybko zbieżne do zera). Parametr p natomiast najlepiej wziąć taki, żeby „długość fali” była kilkukrotnie mniejsza od rozmiarów studni. Za duży pęd, spowoduje, że trzeba będzie zliczać zbyt dużo składowych.

Napisany przeze mnie iloczyn skalarny (φ_n, ψ_t₌₀) to całka po odcinku (0, L). Da się policzyć, ale wzór wyjdzie paskudnie długi. Zauważmy jednak, że dla odpowiednio dobranego M i q poza odcinkiem całkowana funkcja jest o rzędy wielkości mniejsza od tej w odcinku, więc zamieniłem sobie całkę po odcinku na cąłkę po całej prostej i wynik wyszedł o wiele prostszy. Obliczone wielkości a_n=(φ_n, ψ_t₌₀) są następujące:

$an ~ (e^{-{(p/ħ+k)^2/2M+i(p/ħ+k)q}- e^{-{(p/ħ-k)^2/2M}+i(p/ħ-k)q})$

Wektor falowy k zależy od liczby kwantowej n: k=nπ/L.

A skąd wziąć ruchome obrazki?

Z Excela to już chyba nie za bardzo, bo trzeba by było urządzić sobie tabelkę o rozmiarach „liczba składowych” na „liczba punktów wykresu” plus współrzędne wektora początkowego i fazy. Kiedyś, za czasów kiedy programowanie w Turbo Pascalu należało do dobrego tonu wśród studentów niekoniecznie informatycznych, rozwiązanie byłoby oczywiste: Napisać program.

Nawet nie zastanawiałem się czy Freepascal zrobi to co chciałem, bo powoli zapominam pasakalowe sztuczki i skierowałem swoją uwagę na potężne, choć darmowe, narzędzie Microsoftu czyli na Visual C++ EE. Narzędzie to pozwoli na utworzenie programu okienkowego, w którym będziemy malować bitmapę i wyświetlać ją na formie (okienku).

VC++EE ma sprawnie działający system podpowiedzi i dzięki niemu szybko okaże się, że obiekt typu Bitmap ma niewiele metod, którymi można zmienić przechowywany przez siebie obrazek – doliczyłem się jednej funkcji SetPixel() – a mam namalować linię. Malowanie po bitmapie robione jest na mój amatorski gust naokoło, to znaczy trzeba sobie zdefiniować obiekt Graphics i to on będzie zarządzał bitmapą. Takie to javowe, ale może się nie znam.

Drawing::Bitmap ^bitmapa = gcnew Drawing::Bitmap( tlo ); Drawing::Graphics ^g = Drawing::Graphics::FromImage( bitmapa );

Teraz spokojnie można rysować sobie linie. Po narysowaniu wykresu można wyświetlić taką bitmapę na formie, pakując ją do obiektu typu PictureBox.

g->DrawLine( pen, xp, yp, xk, yk ); ... pictboxWykres->Image = bitmapa

C++/CLI wygląda jak dwa języki programowania, żyjące sobie trochę osobno. Klasyczne obiekty C++ mają się nijak do obiektów z CLI. No i w tym jest ambaras, bo one oba nie chcą naraz. Choćby liczby zespolone z C++owej biblioteki <comlex> są strukturami, a tych zbiorniki typu Collections::Generic::List<> nie chcą przechowywać. Jedyna rada, to albo napisać sobie swoją klasę zespolone, albo posługiwać się wskaźnikiem, który jest łaskawie tolerowany przez gc-owe klasy. Akurat w tym przypadku, to w jakimś sensie zaleta, gdyż całość obliczeń lepiej schować sobie do osobnego, czysto C++owego obiektu, który byłby dostępny dla formy C++/CLI właśnie poprzez wskaźnik. Forma ma służyć przecież tylko do pokazywania obrazków, a nie obliczeń – obowiązuje separacja kodu.

Znów się rozpisałem, tym razem o programowaniu (szczególnie, że jest amatorskie), a przecież wszyscy już niezdrowo podnieceni, czekają, aż pokażę ruchome obrazki.

Filmy

Przez trzy ostatnie notki nie przejmowałem się zupełnie podstawianymi parametrami. Chodziło mi tylko o utworzenie ruchomych obrazków, więc np. gdybym dla cząstki swobodnej wziął inną masę, to i tak musiałbym tak dobrać skale (czasową i przestrzenną), żeby widoczny był efekt rozpływania i przesunięcia paczki falowej. W tym przypadku, trzeba trochę uważniej. Przede wszystkim szerokość paczki falowej powinna być (załóżmy, że chodzi o potrójne σ) co najmniej dwa razy mniejsza od szerokości studni. Pisałem o tym kilka akapitów wyżej.

Warto również tak dobrać pęd, żeby choć trochę paczka poodbijała się od ścian zanim się rozpłynie. W programie tak dobrałem b, żeby „długość fali” była ok. 1/15 szerokości studni, co widać na poniższym obrazku przedstawiającym część rzeczywistą stanu początkowego ψ(x):

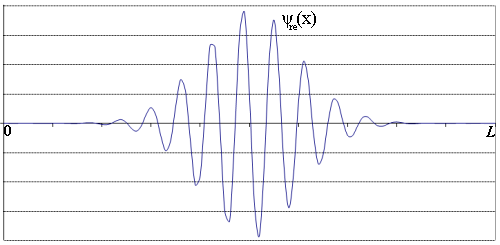
Jeszcze słowo o pędzie początkowym. Im większy pęd, tym więcej składowych trzeba policzyć – im większa energia paczki, tym wyższe składowe będą istotne. W powyższym przypadku starczyło 50 składowych. Wykres pokazujący współrzędne (część rzeczywistą i urojoną) stanu początkowego pozwala mniemać, że składowe n>50 i tak są znikomo małe.

Największy problem niniejszej notki, to jednak nie kłopoty rachunkowe czy pisanie programu, a czas. To znaczy taka ilość kroków czasowych (klatek filmu), żeby to co się widzi było jeszcze ruchome. Poprzednio wystarczało 20-30 klatek, do oscylatora wziąłem 50 klatek, żeby wrażenie ruchu było lepsze, szczególnie, że „filmik” był zapętlony. W przypadku odbijania od dwóch ścian też można sobie zapętlić odtwarzanie, ale czas powrotu do stanu początkowego będzie o wiele dłuższy.

Klasycznie piłka odbija się od jednej, potem od drugiej ściany i sytuacja wraca do stanu początkowego. Tu tak nie będzie. To znaczy, po iluśtam odbiciach paczka falowa wróci do stanu początkowego, ale nie zależy to w ogóle od funkcji falowej! Akurat dla nieskończonej studni, czas powrotu będzie czasem, po którym do stanu początkowego przejdzie pierwsza składowa czyli exp{-iE₁T/ħ}sin(πx/L). Trzeba odczekać, żeby faza przeszła cały zakres 2π. Jak podstawimy wartość E₁, wyjdzie czas: T=4mL²/ħπ. W stosunku do zmian paczki falowej – obejmujących kolejne odbicia – to bardzo długo. Przypadkowo może się zdarzyć, że czas będzie krótszy – na przykład kiedy nieparzyste współrzędne będą zerowe, będzie on cztery razy krótszy, ale przypadki takie to „zbiór miary zero” jak mówią fizycy.

Absolutne minimum, żeby widzieć kolejne zmiany, to 1000 klatek. GIF tego już nie uciągnie. Dlatego zastosowałem mało finezyjną metodę umieszczając… filmik na YouTube. Uruchomiłem program, ustawiając 4000 klatek, co dało nieco ponad 4 minuty przechwytywania kawałka ekranu.

A co widać? Jak zmienia się w czasie |ψ(x)|². Przede wszystkim paczka odbija się od ścian, efektownie interferując (część odbita dodaje się do tej jeszcze nie odbitej). Drugim efektem jest rozpływanie się paczki. „Rozpłynięte” ogony też się odbijają i dodatkowo interferują. Po pewnym czasie obrazek jest dość chaotyczny, że użyję takiego określenia. Aż dziw bierze, że po wspomnianym czasie powrotu te rozpłynięte, poodbijane kawałki zlewają się na powrót w kształtną paczkę. W połowie czasu powrotu T paczka „odzyskuje” swoją postać, ale ma przeciwnie skierowany kierunek ruchu w stosunku do początkowego.

Dla ciekawości wziąłem sobie paczkę o bardzo malutkim średnim pędzie, czyli prawie „nieporuszającą się”. Jak odczekamy te cztery minuty, to też wróci do stanu początkowego. Ten filmik jest mniej efektowny, ale może komuś starczy cierpliwości, by doczekać do końca.

No i niestety notka wyszła długa. Następne powinny być krótsze.

Dopisane później...

Lekko zmodyfikowałem program na „życzenie” BJABa i pokazuję paczkę falową, to znaczy: część rzeczywistą na niebiesko i urojoną na czerwono. Paczka zaiwania, że czasami niewiele widać, ale można przynajmniej zauważyć dwie rzeczy:

jak paczka porusza się bez dodatkowych „efektów”, to część urojona „wyprzedza” rzeczywistą o świerć długości fali;
tam gdzie paczka interferuje faza jednej części jest zgodna lub przeciwna (pół długości fali) względem drugiej.

Ale to proste obserwacje, których w zasadzie można było się domyślić. Szybkość zmian fazy w danym punkcie nie jest wbrew pozorom wielkością mierzalną, bo przeskalowując energię o stałą zmieniamy również szybkość zmian fazy.