Stany mieszane klasycznie

Ostatni wykład z analizy matematycznej przed feriami. Większość studentów rozjechała się już do domów, na sali niedobitki. Wspomniany tu już kiedyś prof. Zbigniew Oziewicz stwierdził, że nie ma sensu wprowadzać nowego materiału, więc gratisowo opowiedział, tak od serca o różnych rzeczach. Oprócz uwag o (bez)sensowności stosowanych powszechnie formalizmów matematycznych, uraczył słuchaczy opowiastką o mechanice kwantowej. To wtedy dowiedziałem się, że prawdziwe stany, to nie są wektory z przestrzeni Hilberta. A skoro sam Oziewicz tak mówił to znaczy, że rzecz jest warta uwagi. Ponieważ kurs mechaniki kwantowej przewidziany był w następnym roku, cała sprawa musiała poczekać.

Owe prawdziwe stany to macierze gęstości, nazywane również stanami mieszanymi. Żeby nie myliły się, stany z jakimi do tej pory mieliśmy do czynienia (np. funkcje falowe) nazwę stanami czystymi.

Wydaje mi się, że najlepiej wytłumaczyć istotę macierzy gęstości, poprzez analogię do mechaniki klasycznej, bo tam też istnieją podobne twory. Piszę „mechanika klasyczna”, ale w tej notce używam tzw. podejścia hamiltonowskiego.

Jak to jest w mechanice klasycznej?

Zacznijmy od przestrzeni stanów czystych. Fizycy mówią na to: przestrzeń fazowa. Każdy stan czysty to położenie i pęd. Dla N cząstek będzie to punkt mający 6N współrzędnych – na każdą cząstkę przypadają trzy współrzędne położenia i trzy składowe pędu[1]. Ponieważ jednak ilość wymiarów nie jest istotna dla dzisiejszej pogadanki zamiast wypisywać 6N współrzędnych, stany czyste zapiszę symbolicznie jako (p, q), choć kilka poniższych przykładów będzie dotyczyć jednej cząstki. Czyli w tym przypadku p oznaczać będzie składowe p_x, p_y i p_z, a q to skrótowo zapisane x, y, z.

(p_x, p_y, p_z, x, y, z) ≡ (p,q) ∈ Γ

Fizyk, jak już napisze sobie jaką ma przestrzeń fazową, dobierze sobie jakiś stan początkowy i obliczy jak będzie się zmieniać. Obliczy, czyli rozwiąże równania Hamiltona – „przetworzone" równania Newtona. Jest to główny cel pisania takich równań: jak będą wyglądać położenie i pęd w przyszłości (i w przeszłości zresztą też):

ewolucja stanu klasycznego

Teraz pora na obserwable. Jak pamiętamy, obserwable to inaczej wielkości fizyczne (pęd, energia, moment pędu i co tam jeszcze co da się wyrazić za pomocą pędu i położenia). Kolejny raz narzekam, że ktoś pewnie wybrał taką nazwę, żeby trudniej było się zorientować o co chodzi. Taką wielkością może być na przykład energia kinetyczna:

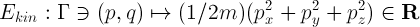
Ekin: Γ ∋ (p,q) ↦ (1/2m)(px2+ py2+ pz2) ∈ R

Zapisałem to tak, żeby było widać, że w tym ujęciu energia, to funkcja na przestrzeni stanów czystych: każdemu punktowi (p,q) przyporządkowuje liczbę rzeczywistą. No to jeszcze jeden przykład takiej obserwabli – składowa momentu pędu w kierunku Z:,

$J_{z}: \Gamma \ni (p,q) \mapsto xp_y- yp_x \in {\bf R}$

Wyłania się pewna ogólna prawidłowość: obserwable należą zbioru do rzeczywistych funkcji, których dziedziną jest przestrzeń stanów czystych. Oznaczę sobie taki zbiór przez A. Żeby zabawa miała sens, to funkcje z A muszą spełniać pewne warunki, które ściśle i dokładnie są znane chyba tylko ekstremistom matematycznym. Tu o nich na szczęście pisać nie będę.

Jak jeszcze nie odpłynąłeś do tej pory, duża szansa, że uda ci się wytrwać do końca. Powyższy formalizm pozwolił obliczyć trajektorie statków i sond kosmicznych, więc taki zły nie jest, ale to nie znaczy, że nie da się go ulepszyć ☺.

Na przykład, jak rozsądnie oszacować np. energię kinetyczną, jeśli nie znamy dokładnie stanu czystego? Załóżmy, że znamy tylko prawdopodobieństwo, że nasz układ będzie w danym stanie czystym. Wszyscy co znają pojęcie średniej ważonej od razu powiedzą, żeby owe prawdopodobieństwa potraktować jak wagi i obliczyć średnią ważoną szukanej wielkości fizycznej.

Czyli: jeśli μ_i oznacza prawdpodobieństwo, że układ jest w stanie (p_i, q_i) to wartość średnia przykładowo energii kinetycznej równa jest:

$<E> =\sum_i (μ_i p_i^2)/2m$

Dla dowolnej funkcji f(p,q) i dla „pomieszanego” stanu opisanego przez zestaw prawdopodobieństw μ_i można zastosować wzór:

$<f> =\sum_i μ_i f(p_i, q_i)$

Żeby powyższe wzory pokazywały średnią ważoną, wagi czyli prawdopodobieństwa muszą sumować się do jedynki: ∑_i μ_i =1.

Wybrałem literkę μ, pomimo, że zwykle na prawdopodobieństwo stosuje się literkę p. Ale w notce p akurat oznacza pęd, więc mogłoby się to mylić. Po drugie literkę μ matematycy czasami oznaczają miary. Jak miałeś do czynienia z miarami, to pewnie zgadniesz, że μ nie musi być dyskretne, może być ciągłe, albo nawet jeszcze jakieś nietypowe, byleby było miarą.

$<f>= \int_\Gamma f(p,q) d\mu =\mu(f)$

To zapis hard, rodem z książki Maurina, czasami wygodnie pomyśleć sobie, że miara jest rozkładem ciągłym μ(p,q):

$<f> = \int_\Gamma f(p,q) \mu(p,q) dpdq$

Żeby μ(p,q) pasowało, musi być dodatnie i sumować się do jedynki:

μ(p,q) ≥ 0 oraz ∫_Γ μ(p,q)dpdq = 1

Ale matematycy wiedzą, że zbiór miar jest bogatszy od skończonych sum μ_i i rozkładów ciągłych μ(p,q). Takie obiekty jak miary probabilistyczne, określają jako funkcje liniowe, których dziedziną jest zbiór funkcji A (obserwable)[2]. Zbiór takich funkcji oznaczę tą samą literką tylko z „primem”: A’. W żargonie mówi się, że to przestrzeń dualna do A. No i teraz mamy w końcu definicję macierzy gęstości w mechanice klasycznej: Są to elementy z A’, dodatnie i sumujące się do jedynki. Tylko w przypadku klasycznym mówi się raczej o stanach mieszanych, bo przecież nie są one macierzami.

Ściślej rzecz biorąc, zbiór A’ zawiera wszelkie możliwe stany: mieszane i czyste. Jak wygląda w tej terminologii stan czysty? To delta Diraca. Wartość obserwabli f w stanie czystym (p₀,q₀) da się zapisać jako działanie takiej delty na funkcję f:

$μ_(p_0,q_0): A \ni f -> \int_\Gamma f(p,q)\delta(p-p_0, q-q_0) dpdq = f(p_0,q_0) \in R$

W przypadku ciągłych rozkładów prawdopodobieństwa μ(p,q) będziemy mieli wzór:

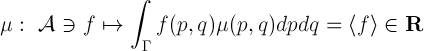
μ : A ∋ f ↦ ∫Γ f(p,q) μ(p,q) dpdq = <f> ∈ R

Na rysunku poniżej widać czym różni się stan czysty – całe prawdopodobieństwo skoncentrowane w jednym punkcie (p₀,q₀):

od stanu mieszanego, gdzie mamy rozkład prawdopodobieństwa:

Podsumowanie

Przeczytałem jeszcze raz powyższe wypiski i chciałoby się zakrzyknąć za panem Temperą „Abstrakcja, czysta abstrakcja!”. Ale fizycy teoretycy czasami tak mają, że idą od ogółu do szczegółu. Jeśli notka była zbyt abstrakcyjna i nic nie zrozumiałeś, to pomyśl o stanach mieszanych jako o wagach potrzebnych do obliczania średniej ważonej. To podstawowa idea. Reszta notki, to próba matematycznego uściślenia tej idei.

* * *

Żeby nie było, że stany mieszane czyli rozkłady prawdopodobieństwa na przestrzeni fazowej do niczego nie służą: Równania ruchu, czyli równania Hamiltona można przetworzyć tak, by dotyczyły stanów mieszanych. Oznacza to, że możemy spodziewać się ewolucji czasowej stanów mieszanych:

ewolucja stanu mieszanego

* * *

Notka przydługawa, ale co zrobić… Jak to jest w kwantówce, napiszę w kolejnym odcinku, a teraz jedynie podsumowanie w tabelce:

tabela

Jak nie jesteś matematykiem i nie odfrunąłeś możesz sobie pogratulować.

[1] Fizycy wiedzą, że: współrzędnych na przestrzeni fazowej może być dowolna, parzysta ilość; współrzędne te nie muszą być wcale kartezjańskie; i jeszcze wiele innych rzeczy. Ale w tej notce akurat to nie jest ważne, więc zostanę przy „zwykłym” pędzie i położeniu.

[2] Proszę wybaczyć ten „skrót myślowy”. Miary w analizie matematycznej definiowane są inaczej. To że ich zbiór jest dualny do specjalnie dobranego zbioru funkcji, załatwia dopiero twierdzenie.