Kartezjański układ współrzędnych – najprostszy sposób na określenie współrzędnych punktu: długość, szerokość i wysokość. Trzy proste ułozone względem siebie pod kątem prostym.
Mówi się, że prawa fizyki nie zależą od układu współrzędnych. Ale czasami trudno je zapisać, jeśli nie korzysta się właśnie z układu kartezjańskiego. Weźmy zwykłą drugą zasadę dynamiki Newtona. Napisanie odpowiednich równań różniczkowych nie nastręcza kłopotów:
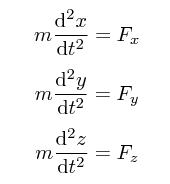
Ciekawe jednak czy ktoś podejmie się je napisać dla jakiegoś nieprostokątnego układu współrzędnych? Trudne. Jedyna droga, to powyższe równania jawnie przeliczyć.
I tu ciekawostka: w XIX wieku udało się sformułować równania ruchu mechaniki klasycznej dla dowolnego układu współrzędnych przestrzeni konfiguracyjnej. Równania te nazywane są równaniami Hamiltona[1], choć nie wszystkie siły da się w ten sposób uwzględnić (na przykład siły tarcia). To „efekt uboczny” poszukiwań pewnych własności równań ruchu (np. wielkości stałych w czasie – całki ruchu), dzięki którym łatwiej rozwiązać same równania.
Swoje trzy grosze dołożyła elektrodynamika. Wynikająca z niej szczególna teoria względności dodała do trzech wymiarów przestrzennych również czas. No i skutkiem tego taki czterowymiarowy układ kartezjański okazał się dodatkowo inercjalny[2]. Ale wracając do tematu również i równania Maxwella zapisano w końcu dla dowolnego układu, choć żeby coś mądrego powiedzieć o polu e-m to i tak na koniec trzeba je wyrazić w jakichś prostokątnych współrzędnych.
Jest jednak teoria, która jakoś nie pozwala za bardzo wyjść poza układ x, y, z. To mechanika kwantowa. Wbrew formalnemu podobieństwu do formalizmu Hamiltona, równania Schrodingera mechaniki falowej pisze się dla „zwykłej” trójwymiarowej przestrzeni, a później obcina do dwóch czy jednego wymiaru albo zamyka w jakimś pudełku[3]. Inne przypadki? Trzeba kombinować i nie zawsze się uda.
Przykład: W mechanice klasycznej możliwy jest do opisania modelowy jednowymiarowy ruch koralika nanizanego na sztywną „nitkę” w kształcie okręgu. Matematyczny formalizm mechaniki kwantowej nie dopuszcza jednak do skwantowania współrzędnej φ (kąt) i sprzężonego do niej pędu j (moment pędu). Sam byłem zaskoczony, kiedy znalazłem dowód na to w jednej z książek[4].
Czy więc kartezjański układ jednak jest jakoś wyróżniony? Może i tak, ale z drugiej strony ogólna teoria względności w zasadzie pozbyła się prostych czasoprzestrzeni rodzaju Rn, w których tensor metryczny miałby współrzędne ±1. Można powiedzieć, że pozbyła się układów kartezjańskich.
Niby układ współrzędnych to czysto techniczna sprawa, powinna być „przezroczysta” jeśli chodzi o prawa fizyki. Ale chyba nie jest tak do końca.
[1] Równania opisują ruch w dowolnych współrzędnych, a każdej z nich odpowiada tzw. pęd kanoniczny (zwany też uogólnionym) - np. dla kąta jest nim moment pędu. Za nim Hamilton napisał te swoje równania, po drodze był jeszcze formalizm Lagrange'a, ale to dłuższy temat.
[2] W równaniach Newtona wystarczyło dodać tzw. siły bezwładności, żeby poprawnie wyliczyć ruch w układzie nieinercjalnym.
[3] Można oczywiście przeliczyć sobie jak będzie wyglądał operator energii H=-(ħ2/2m)Δ +V(r) w innych układach, ale chciałoby się wziąć hamiltonian z mechaniki klasycznej (to funkcja od tzw. uogólnionych położeń i pędów) i mieć jasne zasady jego kwantowania, czyli napisania operatorowego odpowiednika kwantowego.
[4] Walter Thirring „Fizyka matematyczna”

