Żyjemy w czasach pisma obrazkowego. Żeby nie zostać w tyle, dziś próba dotrzymania biegu czasom. Szczególnie, że fajnie się ogląda obrazki z funkcjami falowymi. Tyle się mówi, że nie można zobaczyć tych maleńkich obiektów opisywanych mechaniką kwantową, więc możliwość obejrzenia jak wyglądają wielkości matematyczne opisujące te obiekty jest jak najbardziej atrakcyjna.
Funkcja falowa
Mechanika kwantowa mówiąc o cząstkach, używa funkcji falowych ψ(r). Ich dziedziną jest przestrzeń położeń – czyli dla jednej cząstki będzie to najzwyklejsza przestrzeń trójwymiarowa R3. Jednak ze względu na popularyzatorskie ujęcie wymuszające prostotę, ograniczę się do jednego wymiaru i będę rozpatrywał ψ(x). Mimo to, osoby o zacięciu matematycznym mogą sobie wszystkie wyniki, pokazane w tej i następnych dwóch notkach, przełożyć do trójwymiarówki.
Pora na kilka własności takiej funkcji. Wartości funkcji nazywane są dla niepoznaki amplitudami prawdopodobieństwa i nie dają się zmierzyć. Znaczenie fizyczne posiada natomiast |ψ(x)|2 – jest to gęstość prawdopodobieństwa znalezienia (pomiaru) cząstki w punkcie x. We wzorze powyżej użyto symbolu wartości bezwzględnej (modułu), bo wartości funkcji falowej są zespolone, a prawdopodobieństwo musi być nieujemne.
No to spójrzmy na funkcję falową ψt(x). Indeks t oznacza, że będzie ona się zmieniać w czasie. Czyli obiecane we wstępie obrazki powinny się poruszać! Funkcja taka podlega równaniu Schrödingera:

Teraz trzeba rozwiązać to równanie, zakładając jakąś początkową postać funkcji falowej ψ0(x). Patrząc na powyższe równanie nie wydaje się, żeby to było jakieś łatwe, ale spróbujmy zaprząc do pracy…
Gaussowskie paczki falowe
W jednej z notek rozpisywałem się o takich stanach, dziś trochę inne podejście. Tu określę je następująco:
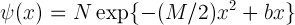
gdzie M, b są liczbami zespolonymi. Żeby funkcja taka była normowalna reM>0. Całkując |ψ(x)|2 po wszystkich x otrzymamy warunek na stała normującą N:

Mając taką funkcję, możemy obliczyć sobie średnie położenie i pęd:

Stany takie mają jeszcze jedną przyjemną właściwość. Otóż jeśli energia potencjalnaV(x) jest wielomianem co najwyżej drugiego rzędu w x, i stanem początkowym jest stan gaussowski, to rozwiązanie równania Schrödingera też jest stanem gaussowskim dla każdego t.
Powyższe zdanie wygląda jak twierdzenie, więc wypadałoby je udowodnić. Coś w rodzaju dowodu ukaże się przy rozwiązywaniu tegoż równania. Na początek weźmy najprostszy przypadek, czyli cząstkę swobodną: V(x)=0. Zgadujemy rozwiązanie jako (normowanie wtłoczone zostało do wykładnika eksponenty):

Podstawmy je do równania, a otrzymamy (kropki nad literkami oznaczają różniczkowanie po czasie):

Po podzieleniu obu stron równania przez ψ i porównaniu współczynników przy tych samych potęgach x, dostanę równania różniczkowe na M i b. Członem g się nie zajmuję, bo odpowiada on normowaniu – już znalezione; i fazie – jest nieistotna.

Rozwiązując je, otrzymamy rozwiązanie ψt. Jest ono określone przez zespolone parametry Mt i bt. Widać od razu, że ponieważ rozwiązanie jest określone jednoznacznie i startujemy z dowolnych b0 i M0, udowodniliśmy to twierdzenie dla stałego potencjału. Podobnie da się policzyć dla potencjałów co najwyżej kwadratowych. Tego triku nie da się zastosować już w przypadku potencjału rzędu trzeciego. A oto rozwiązania:

Teraz nie powinno być kłopotów, żeby namalować sobie jak się będzie zmieniać funkcja falowa w czasie. Trzeba jedynie podstawić sobie te wartości do wzoru (*) i namalować wykresy dla kilku czasów t. Na osi poziomej mamy położenie, na pionowej |ψt(x)|2 czyli gęstość prawdopodobieństwa. Mnie wyszło coś takiego:

Widać nie tylko przesuwanie się paczki (ruch swobodny) ale i „rozpływanie” się prawdopodobieństwa. Jest to typowe zachowanie dla cząstek swobodnych, niezależnie od wyboru stanu początkowego ψ0, po pewnym czasie „rozpłynie” się on (a dokładniej to gęstość prawdopodobieństwa) po dowolnie dużym obszarze.
Uwagi dla szczególarzy
Przy określaniu warunków początkowych można brać dowolne M0 i b0. Do powyższej animacji wziąłem jednak rzeczywiste M0, by mieć jasną interpretację, gdzie jest informacja o szerokości paczki (nieoznaczoności położenia). Za to b0 było czysto urojone, co odpowiada przypadkowi gdy cząstka jest ulokowana w początku układu współrzędnych - część rzeczywista równa zero. Natomiast urojone b0 to pęd przeskalowany o stałą Plancka.
Ruchomy obrazek uzyskałem w dwóch krokach: Wykresy namalował mi Excel, a poskładałem je w całość przy pomocy programu GIMP. Jak zmusić Excela do obróbki liczb zespolonych, to już może w następnej notce.
Można nieco uprościć wzór na |ψt(x)|2 zamiast podstawiać na wprost przeliczone M, b do (*) i brać z tego moduł do kwadratu. Uproszczona formuła wygląda następująco:

Ale przy założeniu, że całość i tak liczy Excel, może nie być to istotnym ułatwieniem.
Wartości średnie położenia i pędu są takie same jak w klasycznym ruchu bezwładnym. Niekoniecznie jest to widać na pierwszy rzut oka, gdyż zależność od czasu dla M i b tkwi w mianowniku, a średnie położenie zależy liniowo od czasu.
Wspomniane „rozpływanie” paczki widoczne jest dla „nieruchomej” cząstki, czyli dla im b0=0.

W obu przypadkach, przedstawionych na ruchomych obrazkach, startowałem od stanów minimalizującej zasadę nieoznaczoności dla pędu i położenia – co matematycznie oznacza, że M miało tylko część rzeczywistą. Ewolucja czasowa to psuła. Gdyby wziąć takie M0, że imM0≠0, to oznaczałoby to, że albo stan gdzieś w przeszłości minimalizował zasadę Heisenbera, lub zrobi to w przyszłości. Tak czy siak, jak dostatecznie długo poczekamy, to na pewno się „rozpłynie”.
Zachęcam do samodzielnej działalności.

