Nerwowy spacer w kwantowej studni (obrazki)

Miałem już skończyć prezentację ruchomych paczek falowych w poprzedniej notce, ale w komentarzu do niej, SNAFU podał ciekawy pomysł na zbadanie zachowania pewnej funkcji falowej w nieskończonej studni potencjału: W chwili t=0, po nagłym wzroście szerokości studni z L do 2L, funkcja ψ(x) w przedziale od 0 do L ma postać sinusa, a między L i 2L mamy ψ(x)=0. No i trzeba zbadać ewolucje tej funkcji w czasie, przez rozłożenie tej opisanej powyżej funkcji ψ na szereg Fouriera, który można uważać za stan superpozycyjny, kombinację liniową wszystkich możliwych stanów własnych – no i obliczyć każdy stan własny dla chwili t>0 i później „złożyć” na powrót te wszystkie stany, żeby dostać „wypadkową” funkcję ψ dla tego t. Ja przed 18 laty zrobiłem taką animację (…) Ciekawe było to, że funkcja ψ(t) „szalała”, przyjmowała jakieś strasznie chaotyczne kształty, żeby po pewnym czasie zmienić się w idealne „lustrzane odbicie” ψ(t=0), a po upływie drugiego takiego samego okresu wracała idealnie do początkowego kształtu ψ(t=0).

Ciekawe, ciekawe… Rzeczywiście, aż żal, żeby nie skorzystać z gotowego programu i nie policzyć sobie jak będzie ewoluować połówka stanu stacjonarnego. Cały formalizm potrzebny do wykonania zadania pokazałem już w poprzedniej notce, więc nie będę go tu powtarzał.

Niezbędna matematyka

Jak wygląda taki stan stacjonarny w „rozciągniętej” studni? Dla ustalenia uwagi, na rysunku widoczny będzie stan o najniższej energii – wygląda jak połówka stanu k=2, natomiast wzory będę wypisywał dla dowolnego k.

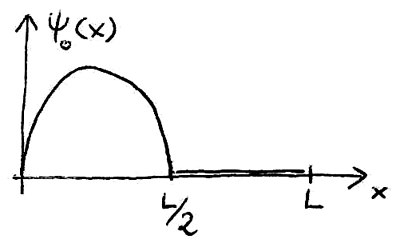
połówka sinusa

Użyję nieco innej nomenklatury niż SNAFU: zamiast mówić o stanie stacjonarnym, dla którego studnia się poszerzyła z L do 2L, będę mówił o połówce parzystego stanu stacjonarnego w studni o szerokości L. Teraz taki stan trzeba rozłożyć w bazie wektorów własnych energii, by znaleźć współrzędne początkowe. Iloczynem skalarnym będzie całka:

$(ψk, Φn) ~ \int_0^{L/2} \sin(π n x/L)\sin(π k x/L)dx$

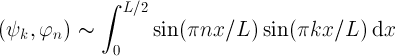
Można ją policzyć (po drodze trzeba zamienić iloczyn sinusów na różnicę cosinusów) i wzór końcowy wyjdzie następujący:

$an ~ π dla n=k i {2\over n+k}\sin({π(n+k)\over 2}) - {2\over n-k}\sin({π(n-k)\over 2}) dla \ n\not=k$

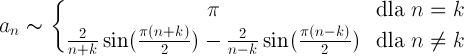
Chodzi o to, żeby do „podstawowego” sinusa trzeba dodać sumę innych sinusów, by wyzerować drugą połówkę funkcji. Na rysunku sytuacja dla stanu k=2:

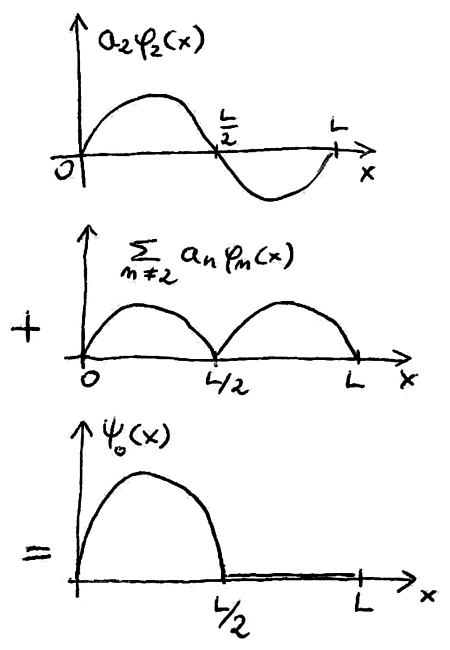
analiza Fouriera połówki sinusa

Zawsze mnie trochę dziwiło, że można sobie złożyć połówkę sinusa z jego harmonicznych, ale to uwaga na boku.

Obrazki

Powyższe wyniki wstawiłem do programu i wyszedł dziwny, nerwowy spacerek. Oto jak dziwnie kolebie się połówka stanu k=2, a dokładniej jej kwadrat modułu. Ponieważ ruchy są zdecydowanie wolniejsze niż ostatnio, przyjąłem sobie 1000 klatek filmu, dzięki czemu trwa on około minuty.

Obrazek nie przypomina łagodnego przelewania się paczki z poprzedniej notki. Dominują nerwowe podskakiwania. To co jest takie samo, to czas powrotu. Jak widać paczka zachowuje się tak, jak we wspomnieniach SNAFU.

Najpierw myślałem, że owe nerwowości są od tego, że wziąłem zbyt mało składowych – na pierwszy rzut oka współrzędne a_n ~ ±(1/n), a z analizy wiadomo, że takie szeregi są wolno-zbieżne (jednak przypatrując się bliżej można zauważyć, że a_n ~ 1/n², więc ze zbieżnością nie będzie tak źle). Więc zamiast 50 wziąłem 200 składowych i… nic się nie zmieniło. Gdyby miał wytłumaczyć te nieregularności w zachowaniu, stawiałbym, że przyczyną jest brzydkie obcięcie stanu początkowego w połowie studni – np. jego pochodna przestrzenna nie jest ciągła. W poprzednim odcinku exp{-x²} skutecznie wygładzała stan początkowy. Na wszelki wypadek sprawdziłem jak poruszają się część urojona i rzeczywista funkcji falowej:

Dla ciekawości zobaczmy jak nerwowo spaceruje sobie połówka stanu o wyższej energii k=6. W sumie podobnie, choć oprócz nieregularnych podskakiwań, widać też łagodne przelewania prawdopodobieństwa.

Spekulacja o pomiarze

Mnie obcinanie połówki stanu skojarzyło się, nie z poszerzaniem obszaru studni, a z pomiarem. Jeśli wymyślę sobie modelowy pomiar dający informację w której części studni znajduje się cząstka (na lewo czy na prawo od środka), to po idealnym pomiarze funkcja falowa stanu stacjonarnego powinna przejść… No właśnie – kiedy wynikiem pomiaru jest „cząstka jest w lewej części studni”, to po pomiarze stan stacjonarny zmieni się w funkcję obciętą, jak sinus powyżej. Symetrycznie będzie dla wyniku „w prawej części”. Obcięty sinus jest „nerwowy”, i jest nadzieja, że może być to jakoś detektowane doświadczalnie. Jak przypomnimy sobie, że studnia nieskończona (w trzech wymiarach) jest modelem elektronów swobodnych w metalu, to kombinując jakiś pomysłowy pomiar, możemy nawet „testować” postulat redukcji pakietu falowego.

Spekulacja naciągana, ale zgodna z postulatami mechaniki kwantowej.