Tak, uważam, że matematyka jest językiem przyrody. A dokładniej tego kawałka przyrody, który jest przez człowieka poznany. Sądzę również, że wbrew temu co się tu i ówdzie czyta, nie jest to nauka zbudowana z abstrakcyjnych pojęć dla samej siebie, a mimo to dzięki swej magicznej sile formalizm budowany przez matematyków nagle okazuje się być przydatny w innych dziedzinach, np. w fizyce.
Powszechnie podnoszonym przykładem tego typu rozumowania, jest historia geometrii nieeuklidesowych. Popularyzatorzy zaczynają od kłopotów z piątym aksjomatem Euklidesa, by przejść do Bolyaiego i Łobaczewskiego. Zwykle kończą na Riemannie i jego geometrii – mamy połowę XIX wieku. A ponad pół wieku później geometria różniczkowa okazuje się być wręcz stworzona na potrzeby einsteinowskiej OTW. Wydaje się, że jest w tym coś magicznego – gotowa teoria leżała sobie odłogiem 60 lat i po tym czasie, nagle i niespodziewanie stała się istotnym elementem jednej z najważniejszych teorii fizycznych XX wieku. Ale jak zdamy sobie sprawę, że formalizm tensorowy, który pozwala okiełznać geometrię riemannowską, „wyprzedza” OTW jedynie kilkanaście lat, co więcej, sprawdza się również dla dziewiętnastowiecznej elektrodynamiki, sprawa wyda się już mniej magiczna.
Matematyka pasuje do rzeczywistości
W ptolemejskim świecie idealna matematyka idealnych okręgów opisywała naturę ciał niebieskich. Nie do końca idealnie, ale i tak mogło to robić wrażenie. Czy ktoś wtedy znał lepszy przykład „pasowania” matematyki do świata rzeczywistego? Okręgi toczyły się jednostajnie po innych okręgach. Dopiero Kepler i Newton zniszczyli ten obrazek. Formalizm zaproponowany przez Newtona był jednak na ówczesne czasy wyjątkowo nieczytelny – nawet w jego otoczeniu niewielu ludzi zrozumiało wyprowadzenia w „Matematycznych zasadach filozofii przyrody”.
Od czasów Newtona wiele czasu jednak się zmieniło i dziś badacze mechaniki klasycznej nie muszą już rysować stada trójkątów i zastanawiać się nad związkami między nimi, by napisać i rozwiązać sobie jakieś równanie różniczkowe. Droga, jaką przeszedł rachunek różniczkowy przez te trzysta lat, pozwala na to, że równania tego typu powinni umieć rozwiązywać wszyscy studenci kierunków technicznych i przyrodniczych. (No dobra, tu trochę odjechałem ☺)
Matematyka a kwantologia
Po co w ogóle piszę te słowa? Bo publikując serię o macierzach gęstości dopuściłem się dużych uproszczeń jeśli chodzi o matematykę. I nie chodzi o zwyczajowe „można udowodnić, ale dowód jest trudny, więc go opuszczę”. Już sam model w którym stany są otworowaniami działającymi na zbiór zawierający obserwable nie jest za bardzo ścisły. I to już dla obrazka klasycznego: Nawet najbardziej grzeczne obserwable mogą nie należeć do zbioru predulanego do przestrzeni miar. Ćwiczenie polegające na skonstruowaniu takiej gęstości prawdopodobieństwa (miary), by nie mogła ona zadziałać na najzwyczajniejszą w świecie energię kinetyczną:
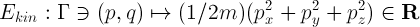
jest proste i daje do myślenia. A przecież w kwantologii jest jeszcze gorzej. Podobne kwiatki wyskoczą już przy okazji stanów czystych.
Można się tym nie przejmować, tylko liczyć. I tu nie ma na co narzekać: kwantologia produkuje zadziwiająco dużo wyników, które nie bacząc, że z matematyką jest na bakier, jak najbardziej sprawdzają się z rzeczywistością. Czy można chcieć więcej?
Można. Chciało by się, żeby stosować poprawną matematykę, która nie zaskoczy jakąś skuchą, tak jak w przypadku wzięcia śladu z reguł komutacji. Da się to zrobić, ale niestety trzeba ostro rzeźbić. Pisałem już kiedyś o tym – dla każdego operatora (obserwabli) konieczne jest określenie jego dziedziny, która jest jedynie podzbiorem przestrzeni Hilberta. Poprawne formułowanie formalizmu mechaniki kwantowej jest trudną i wysublimowaną sztuką[1]. Ilość pracy jaką trzeba włożyć by „uprawdziwić” matematykę kwantów niebezpiecznie przypomina mi zasadę „poprawiania” modelu ptolemejskiego, polegającą do dołożeniu jeszcze jednego okręgu do aktualnie obowiązującego modelu. Na razie…
A może jest tak, jak w przypadku niezrozumiałych w 1687 roku wyprowadzeń Newtona? Może musimy poczekać, by formalizm dorósł i stał się tak samo oczywisty i sprawny, jak równania różniczkowe w mechanice klasycznej? A może odpowiednia teoria już jest gotowa i czeka sobie, jak na Einsteina czekała geometria Riemanna? W dobie nadzwyczaj wąskich specjalizacji i to jest możliwe.
W każdym razie newtonowski związek rachunku różniczkowego i zasad dynamiki budzi we mnie prawdziwy podziw. Być może przyszłe pokolenia będą tak mówić o matematyce w kwantologii.
[1] Zadanie to wykonano tylko dla wersji nierelatywistycznej. Relatywistyka jeszcze czeka – fragment tego zadnia to jeden z kilku problemów milenijnych.

